Introduction
Artificial neural networks are popular to find complex relationships between input data and results. They are useful for solving businesses, medical and academic problems, such as sales forecasting, data mining, cancer detection, and much more.
But neural network training requires a lot of data, time, and computational power. There are two main ways to overcome computation limits and to speed up neural network training: use powerful hardware, such as GPUs or TPUs, or use more machines in parallel.
There are two known ways to split neural network load.
The first one is network parallelism, where layers of the network run on different machines.
The second strategy on how to improve neural network data parallelism, where the whole network (also called the model) runs on each machine, but with different parts of data.
In the last case, it is important to properly split data and ensure that each instance is receiving only a certain type of data, otherwise, the training process is interfered with by new data samples.
Single Feedforward Network
As an example, let build the network based on the crate RustNN, the simple Rust feedforward neural network library with incremental backpropagation training. This library doesn't use any hardware optimization, so the training process may take a long time. For the purpose of some feedback during training, the source code has a callback to indicate status with a progress bar. We are going to implement a classifier for chess moves (part of "fen.txt", described in this article). But it can be any other labeled text data, for example, user intent detection samples.
The code examples below assume you have a basic understanding of Rust programming language.
Clone the repository and build the "single_training" example:
cargo build --release --example single_trainingThe binary is built in release mode to speed-up things.
The used training function is:
fn train(filename: &str, examples: &Vec<(Vec<f64>, Vec<f64>)>) {
let mut net: NN = if std::fs::metadata(filename).is_err() {
NN::new(&[80, 120, 120, 4])
} else {
let mut f = File::open(filename).unwrap();
let mut buffer = String::new();
f.read_to_string(&mut buffer).unwrap();
NN::from_json(&buffer)
};
let example_count = examples.len();
let bar = ProgressBar::new((example_count * EPOCHS as usize) as u64);
bar.set_style(ProgressStyle::default_bar()
.template("{prefix} [{elapsed_precise}] {bar:40} {percent:>3}% - {pos}/{len} - {per_sec} - eta {eta} - {msg}"));
net.train(&examples)
.halt_condition(HaltCondition::Epochs(EPOCHS))
.momentum(0.9)
.rate(0.07)
.go(Box::new(
move |s, epochs, i, _, training_error_rate| match s {
1 => {
bar.set_prefix(&format!("epoch {:>2}", epochs + 1));
bar.tick();
}
2 => {
if i % 1_000 == 0 {
bar.set_position((example_count * epochs as usize + i) as u64);
}
}
3 => {
bar.set_message(&format!("error rate={}", training_error_rate));
bar.set_position((example_count * epochs as usize + i) as u64);
}
4 => bar.finish(),
_ => (),
},
));
let mut f = File::create(filename).unwrap();
f.write(net.to_json().as_bytes()).unwrap();
}
We use 80 inputs in the first layer (sample string max length), two hidden layers with 120 nodes, and 4 output nodes in the output layer (result is 4 char length). Model is persisted in a file, loaded before training, and saved at the end. This allows running the example multiple times to continue learning.
To apply a new network configuration (NN::new(&[80, 120, 120, 4])) you should delete the old network file in the data folder to allow the creation of the new network. Also, as input examples are strings, they are internally converted to vectors of floating numbers with normalization.
Run this example:
./target/release/examples/single_training
The training took 6 minutes. Let's note it.
Parallel Training
As you see, the example above uses only one thread to run. To use more available processor cores, let perform data splitting and run the model in multi-threaded mode.
The incremental backpropagation algorithm here makes it hard to split model (by layers or fit function) between threads, as it requires sequential weights updates. So we split data instead and train the whole model on each thread using part of the original data.
The split function should be stable and feed each instance with certain samples, without any randomness. It is not a requirement in this case, but it speeding up the training process.
The split function is as easy as selecting a thread index by first 9 chars. First, we split examples to n parts:
fn split_examples(
examples: &Vec<(Vec<f64>, Vec<f64>)>,
n: usize,
) -> Vec<Vec<(Vec<f64>, Vec<f64>)>> {
let mut results: Vec<Vec<(Vec<f64>, Vec<f64>)>> = Vec::new();
for _ in 0..n {
results.push(Vec::new());
}
for x in examples {
let s = vec2str(&x.0[..9].to_owned());
let s = s.as_bytes();
let mut num: usize = 0;
for i in s {
num += *i as usize;
}
let idx = num % n;
results[idx].push(x.clone());
}
results
}
and then train the model on n threads with the prepared data parts:
pub fn train_multiple(examples: &Vec<(Vec<f64>, Vec<f64>)>, n: usize) {
let mut pool = Pool::new(n as u32);
let s1 = split_examples(&examples, n);
let m = MultiProgress::new();
pool.scoped(|scoped| {
for i in 0..n {
let example_count = s1[i].len();
let bar = ProgressBar::new((example_count * EPOCHS as usize) as u64);
bar.set_style(ProgressStyle::default_bar()
.template(&(format!("Net #{}: ", i) + "{prefix} [{elapsed_precise}] {bar:40} {percent:>3}% - {pos}/{len} - {per_sec} - eta {eta} - {msg}")));
let pb = m.add(bar);
let v = Arc::new(&s1[i]);
scoped.execute(move || {
let filename = format!("./data/net-{}.json", i);
let mut net: NN = if std::fs::metadata(filename.clone()).is_err() {
NN::new(&[80, 120, 120, 4])
} else {
let mut f = File::open(filename.clone()).unwrap();
let mut buffer = String::new();
f.read_to_string(&mut buffer).unwrap();
NN::from_json(&buffer)
};
net.train(&v)
.halt_condition(HaltCondition::Epochs(EPOCHS))
.momentum(0.9)
.rate(0.07)
.go(Box::new(move |s, epochs, i, _, training_error_rate| {
match s {
1 => {
pb.set_prefix(&format!("epoch {:>2}", epochs + 1));
pb.tick();
},
2 => if i % 1_000 == 0 {
pb.set_position((example_count * epochs as usize + i) as u64);
},
3 => {
pb.set_message(&format!("error rate={}", training_error_rate));
pb.set_position((example_count * epochs as usize + i) as u64);
},
4 => pb.finish(),
_ => ()
}
}));
let mut f = File::create(filename).unwrap();
f.write(net.to_json().as_bytes()).unwrap();
});
}
m.join().unwrap();
scoped.join_all();
});
}
On evaluation, the split function selects the proper sub-network to run:
pub fn run(example_document: String, n: usize) -> String {
let s = &example_document.as_bytes()[0..9];
let mut num: usize = 0;
for i in s {
num += *i as usize;
}
let idx = num % n;
println!("Selected net #{}", idx);
let mut f = File::open(format!("./data/net-{}.json", idx)).unwrap();
let mut buffer = String::new();
f.read_to_string(&mut buffer).unwrap();
let net: NN = NN::from_json(&buffer);
let results = net.run(&str2vec(example_document, 80));
vec2str(&results)
Let build the binary:
cargo build --release --example parallel_trainingand run it:
./target/release/examples/parallel_training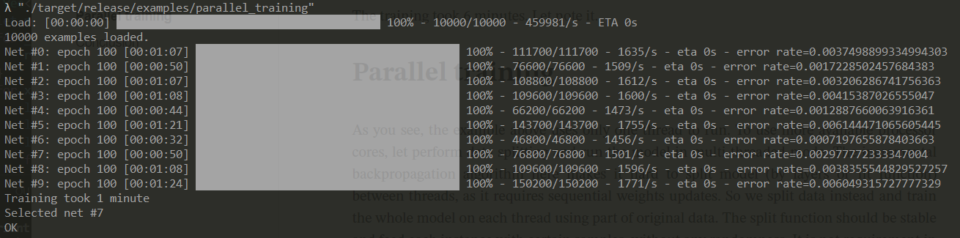
The training took 1 minute. Despite the sum of all the model’s training times is 10 minutes, which is more than the full model time, the result is achieved much faster due to parallelism.
Such a model is nearly ready after 20000 epochs, in opposition to the full model, which requires much more time for training (if not the worse variant when a model cannot finish learning due to luck of nodes or layers).
Data Splitting For the Win!
Data splitting is one of the best ideas on how to speed up neural network training process. As shown above, a group of model instances, trained independently, outperforms one full model by training time, at the same time showing a faster learning rate.
By splitting data into parts and training on multiple threads in this example, we've got about 6 times the speed. If possible to train the model on fewer samples based on the requirements, a simpler network topology becomes available, thus lowering the processing load.
There exist other ideas on how to train neural network faster, such as parallel backpropagation, MapReduce model, and finally, layer distribution, but data splitting has advantages in easier implementation and to be more universal.
With some good data split functions, the amount of input data is no longer a problem. Also, as the split function is handling part of each example, it is possible to reduce the input count. Additionally, this method is available for almost any model type.







